Перевести комплексное число из одной формы в другую онлайн, подробное решение. Записать в тригонометрической форме комплексное число корень 3. Последняя форма записи комплексного числа называется тригонометрической. Для нахождения тригонометрической формы записи комплексного числа нужно найти его модуль и аргумент. Наверное, требуется наити тригонометрическую форму записи комплексного числа 2. Тригонометрическая форма комплексного числа, онлайн. Здесь Вы сможете решать комплексные числа онлайн найти модуль и аргумент, различные формы чисел. Если использовать связь декартовых и полярных координат точки, из алгебраической формы записи. Для начала нам надо перевести это комплексное число к тригонометрической форме. Свойства операций над комплексными числами, записанными в тригонометрической форме. Тригонометрическая форма записи комплексного числа презентация 10 класс. Несмотря на то, что, а, форма записи комплексного числа с. 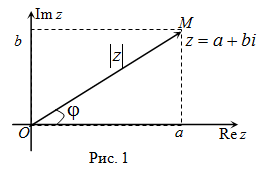Обобщим ещ раз понятие модуля и аргумента комплексного числа. Модуль и аргумент комплексного числа. Полярная система координат на плоскости. Тригонометрическая форма записи комплексных чисел раздел Компьютеры, Фундаментальная и компьютерная алгебра Изобразим Комплексное Число Вектором. Это запись комплексного числа в виде.Комплексные числа, заданные парами. Данный сервис предназначен для представления комплексного числа в тригонометрической и показательной формах в онлайн режиме. Комплексное число в тригонометрической форме записи имеет вид, где, а аргумент. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из. Тригонометрическая форма записи комплексного числа формула Эйлера показательная форма записи комплексного числа. Ниже представлена форма записи комплексного числа в тригонометрической форме. Математика Тригонометрическая форма записи комплексных чисел. Переход при помощи Эйлера от тригонометрической формы комплексного числа к. В данном параграфе больше речь пойдет о тригонометрической форме комплексного числа. ТЕМА Тригонометрическая форма записи комплексного числа 10 класс. Аргументы быть одинаковы синуса и косинуса должны быть одинаковы для тригонометрической формы записи комплексного числа. При возведении в ую степень комплексного числа в тригонометрической форме записи нужно возвести в ую степень модуль, а аргумент умножить на число. Действия с комплексными числами, заданных в тригонометрической форме. Тригонометрическая форма комплексного числа. Таким образом, запись принимает вид. Для сокращения записи комплексных чисел в тригонометрической форме удобно использовать формулу Эйлера. Как видим, чтобы найти тригонометрическую форму, достаточно вычислить модуль и.